Функции Эйлера – это основные элементарные тригонометрические функции, которые широко используются в математике, физике, инженерии и других науках. Они определены как соотношения между сторонами прямоугольного треугольника и углом, образованным этими сторонами. Одной из особенностей этих функций является то, что косинус четный, а синус нечетный.
Четность и нечетность – это свойства функций, которые характеризуют их поведение при замене аргумента на противоположный. Функция называется четной, если ее значение не меняется при замене аргумента на противоположный (т.е. f(x) = f(-x)). Нечетная функция, напротив, меняет знак при замене аргумента на противоположный (т.е. f(x) = -f(-x)).
Итак, косинус – это четная функция, то есть справедливо равенство cos(x) = cos(-x). Это означает, что изменение знака аргумента не влияет на значение косинуса. Например, cos(30°) = cos(-30°), что равно 0.866. Поэтому, когда мы анализируем четность функции косинус, мы можем использовать его значения только для положительных аргументов и затем применить эти значения и для отрицательных аргументов.
Синус, в свою очередь, является нечетной функцией, так как sin(x) = -sin(-x) для любого x. Это означает, что при замене аргумента на противоположный значение синуса меняет знак. Например, sin(45°) = 0.707, тогда как sin(-45°) = -0.707. Поэтому для анализа нечетной функции синус нам необходимо знать значения только для положительных аргументов и, затем, менять знак этих значений для отрицательных аргументов.
Косинус: симметрия и четность

Косинус функции симметричен относительно начала координат - точки (0,0). Это означает, что косинус отрицателен на одинаковых углах находящихся во всех квадрантах. Например, косинус 30 градусов равен 0.866, а косинус 150 градусов равен -0.866. В геометрическом плане, это отражается относительно оси ординат.
Косинус также обладает четностью, что означает, что значение функции изменяется по закономерности при изменении аргумента. В частности, косинус четен относительно начала координат, то есть косинус(-x) = косинус(x), где х - любое действительное число.
Эти особенности косинуса делают его полезным во многих областях математики и физики. Например, в теории колебаний и волн, где важно учитывать фазу и амплитуду.
Понятие четной функции
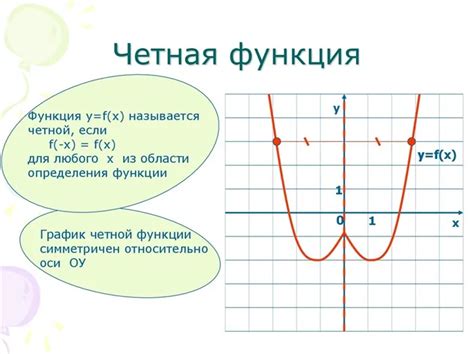
f(-x) = f(x)
То есть, значение функции для отрицательного аргумента равно значению функции для положительного аргумента. Это означает, что график четной функции симметричен относительно оси y.
Косинус является примером четной функции. Для каждого значения x в области определения косинуса выполняется равенство:
cos(-x) = cos(x)
Из этого следует, что график косинуса симметричен относительно оси y.
Четные функции обладают рядом интересных свойств. Например, интеграл от четной функции на симметричном отрезке от -a до a равен удвоенному интегралу от 0 до a:
∫-aa f(x) dx = 2 ∫0a f(x) dx
Понимание четности функций, таких как косинус, является важным для понимания особенностей их применения в математике и науке.
Четность косинуса
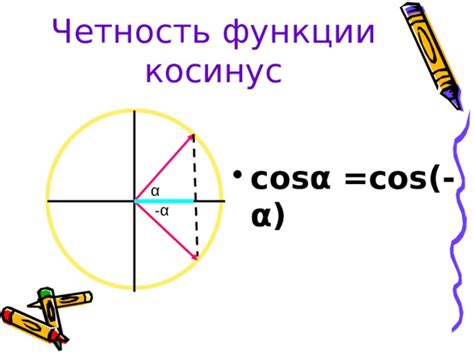
Косинус является четной функцией, что означает, что для любого значения x выполняется следующее: cos(-x) = cos(x).
Это свойство позволяет использовать косинусную функцию для упрощения вычислений и анализа, так как знание значения функции в одной точке позволяет получить значения в других точках.
Например, если нам известно, что cos(30°) = 0,866, то мы можем сразу же получить значение cos(-30°), которое также будет равно 0,866.
С помощью четности косинуса можно также доказать несколько других важных свойств этой функции, например, что cos(180° + x) = -cos(x) или cos(360° - x) = cos(x).
Таким образом, понимание четности косинуса позволяет существенно облегчить работу с этой функцией и применять ее в различных математических и научных задачах.
Косинус и симметрия
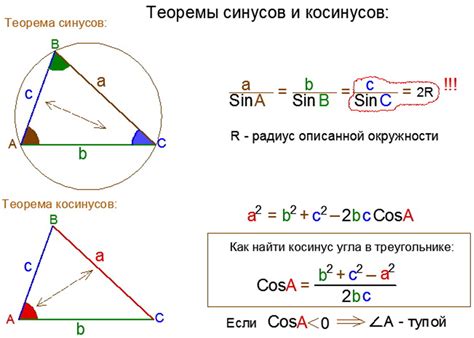
Четная функция обладает свойством симметрии относительно оси ординат. Это значит, что значение функции для отрицательного аргумента равно значению функции для соответствующего положительного аргумента. В случае косинуса, это означает, что cos(-x) = cos(x).
Нечетная функция, в отличие от четной, обладает свойством симметрии относительно начала координат. Это означает, что значение функции для отрицательного аргумента равно значению функции с противоположным знаком для положительного аргумента. В случае синуса, это означает, что sin(-x) = -sin(x).
Интересно, что свойства симметрии косинуса и синуса можно легко объяснить геометрически. Если мы представим график косинуса на координатной плоскости, то можно заметить, что он симметричен относительно оси ординат. А график синуса будет симметричен относительно начала координат.
Синус: антисимметрия и нечетность

Синус функции обычно обозначается как sin(x), где x - это аргумент функции. Основное свойство синуса - его антисимметричность: sin(-x) = -sin(x). То есть, если известно значение синуса при положительном значении аргумента, можно сразу получить значение синуса для отрицательного значения аргумента, просто поменяв знак результата.
Следующее важное свойство синуса - его нечетность: sin(-x) = -sin(x). Это значит, что график синусоиды симметричен относительно начала координат. Если значение синуса при положительном значении аргумента равно y, то значение синуса при отрицательном значении аргумента также будет равно -y.
Антисимметрия и нечетность синуса делают его важным инструментом при решении различных задач из математики, физики, инженерии и других наук. Эти свойства позволяют упростить вычисления и анализ функций, сократить количество используемых формул и сделать математические операции более компактными.
Однако, следует помнить, что данные свойства справедливы только для значений аргументов в радианах, так как синус является тригонометрической функцией, определенной для углов в радианах.
Понятие нечетной функции
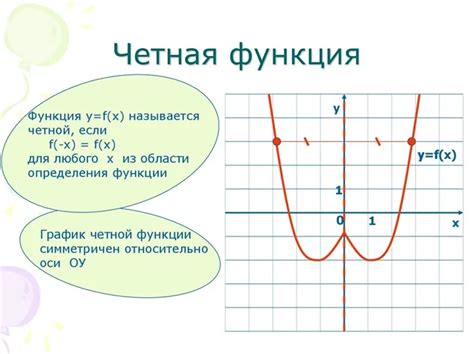
В математике функция называется нечетной, если выполнено следующее условие:
- Для любого отрицательного значения аргумента функции f(-x) = -f(x)
Иначе говоря, если заменить значение аргумента на противоположное, то значение функции также будет иметь противоположное значение.
График нечетной функции симметричен относительно начала координат. Это означает, что с точки зрения графика, функция выглядит одинаково как слева от оси ординат, так и справа.
Примером нечетной функции может служить функция синуса. Для любого числа x выполнено равенство sin(-x) = -sin(x), что и доказывает нечетность этой функции.
Нечетные функции встречаются в различных областях математики и естествознания, и их свойства широко используются для анализа и решения различных задач.
Нечетность синуса

В математике функция называется нечетной, если для любого значения аргумента x выполняется равенство sin(-x) = -sin(x). Это означает, что синус функции является нечетной функцией.
Другими словами, если мы возьмем отрицательное значение аргумента синуса, то получим противоположное по знаку значение этой функции. Например, sin(-x) = -sin(x), sin(-π/4) = -sin(π/4) = -0.7071. Это свойство нечетности делает синус одним из самых важных и полезных математических объектов.
Из нечетности синуса следует, что график синусной функции симметричен относительно начала координат. То есть, для любой точки (x, y) на графике sin(x) справедливо, что точка (-x, -y) также принадлежит этому графику. Это свойство помогает нам предсказывать значения синуса и использовать его в различных математических и физических приложениях.
Важно отметить, что нечетность синуса не следует из его определения или аналитического выражения. Это является свойством, которое можно доказать с помощью математических методов.
Синус и антисимметрия
То есть, если мы построим график синуса, то сможем отметить, что значения функции симметричны относительно оси Oy. Точка (x, y) на графике синуса имеет соответствующую точку (-x, -y).
Также, следует отметить, что антисимметричность синуса приводит к интересному факту: если мы возведем синус в квадрат, то получим равенство sin²(α) + cos²(α) = 1. Это является одним из основных тождеств тригонометрии и неразрывно связано с антисимметричностью синуса.
Особенности функций Эйлера

1. Четность и нечетность
Косинус функция является четной функцией, что означает, что cos(x) = cos(-x). Это означает, что значения косинуса симметричны относительно оси ординат (ось y), что иллюстрируется графиком функции.
Синус функция, напротив, является нечетной функцией, что означает, что sin(x) = -sin(-x). Это означает, что значения синуса также симметричны, но относительно начала координат.
2. Связь функций с геометрическими фигурами
Функции Эйлера тесно связаны с геометрическими фигурами, такими как окружность. Например, значения синуса и косинуса можно интерпретировать как значения x- и y-координаты точки на единичной окружности в полярных координатах.
Это свойство функций Эйлера делает их незаменимыми во многих областях, связанных с геометрией, физикой и компьютерной графикой.
3. Параметры и периодичность
Функции Эйлера имеют два основных параметра: амплитуду и период. Амплитуда отвечает за изменение масштаба функции, а период - за ее повторяемость.
У синуса и косинуса период равен 2π, что означает, что значения функций повторяются через каждые 2π радиан. Это свойство позволяет использовать функции Эйлера для анализа периодических явлений, таких как колебания и волны.
4. Тригонометрические тождества
Функции Эйлера обладают множеством тригонометрических тождеств, которые позволяют выполнять различные преобразования и упрощения выражений, содержащих синус и косинус.
Эти тождества часто используются в математике, физике и инженерных расчетах для упрощения сложных формул и упрощения анализа функций.



