Геометрические фигуры и их свойства всегда восхищали ученых и математиков. Одной из интересных задач геометрии является расчет вписанного угла и его соотношение с дугой окружности. Интересно, что веб-разработчики также часто сталкиваются с этой задачей, когда нужно правильно разместить элементы на странице и рассчитать их относительное положение.
В геометрии вписанный угол определяется как угол, образованный двумя хордами, проходящими через точку на окружности. Оказывается, что такой угол равен половине дуги, на которую он опирается. Для этого достаточно провести отрезки от центра окружности до точек пересечения хорды с окружностью и соединить их с точкой пересечения хорды и ее главной дуги.
Доказательство этого факта основано на том, что угол вписанного угла равен значению накрываемого им сектора окружности, деленного на радиус. С другой стороны, угол главной дуги равен арксинусу отношения половины хорды к радиусу, а дуга окружности равна сумме хорды и ее дуги. Сравнивая данные значения, получается, что угол вписанного угла и половина дуги окружности равны.
Вписанный угол: определение и свойства
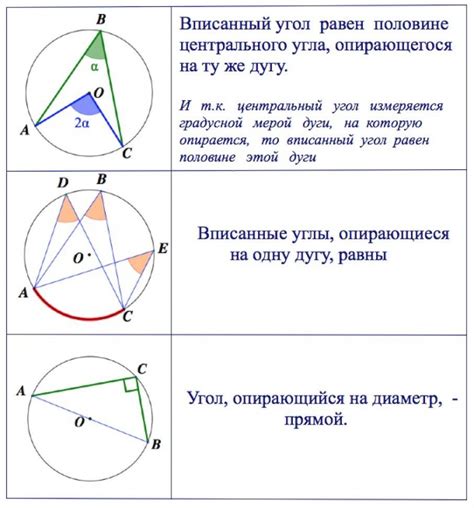
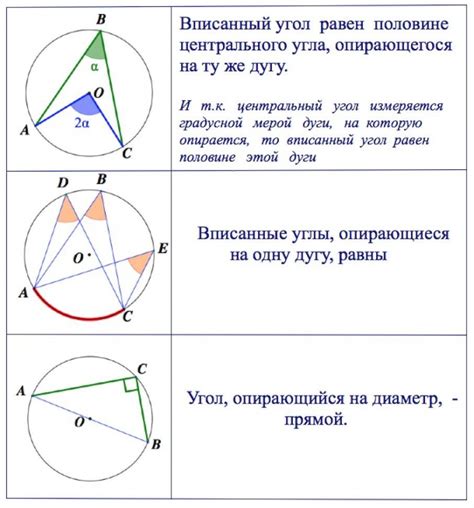
Вписанный угол обладает рядом интересных свойств:
- Вписанный угол равен половине дуги: Угол, опирающийся на хорду и лежащий на окружности, равен половине дуги, заключенной между сторонами этого угла.
- Центральный угол: Вписанный угол является центральным углом, образованным сторонами, пересекающимися в центре окружности.
- Угол, опирающийся на диаметр: Угол, опирающийся на диаметр окружности, всегда является прямым углом.
- Теорема о вписанных углах: Если угол вписан в окружность и сторона этого угла является диаметром, то угол является прямым углом.
Знание этих свойств позволяет решать задачи на нахождение величины вписанных углов и использовать их в доказательствах других геометрических теорем и свойств.
Определение понятия "вписанный угол"
Вписанный угол определяется положением его вершины и дуги окружности, на которую он опирается. Дуга окружности, которая соответствует вписанному углу, называется дугой вписанного угла.
Величина вписанного угла равна половине меры дуги, на которую он опирается. Для вычисления величины вписанного угла можно использовать соотношение: угол = (длина дуги / радиус окружности) * 180°/π.
Теорема: вписанный угол равен половине дуги
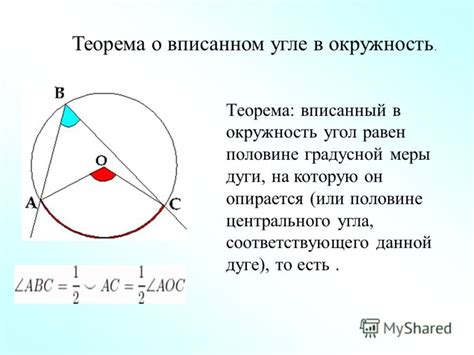
В геометрии существует интересная теорема, утверждающая, что вписанный угол, образованный двумя хордами внутри окружности, равен половине дуги, заключенной между этими хордами.
Предположим, у нас есть окружность с центром O и двумя хордами AB и CD, которые пересекаются в точке P. Вписанный угол, обозначенный как ∠APB, определяется двумя сторонами, которые являются отрезками от точки A до точки P и от точки B до точки P.
Согласно данной теореме, этот вписанный угол будет равен половине дуги ACBD, заключенной между хордами. Другими словами, ∠APB = 1/2 * ∠ACB.
Чтобы доказать эту теорему, мы можем рассмотреть следующие факты:
| 1. | Дуга ACBD – это дуга, которая составляет всю окружность и равна 360°. |
| 2. | Центральный угол, заключенный между хордами AB и CD, является двойным вписанным углом, то есть ∠ACB = 2 * ∠APB. |
- Угол, противостоящий хорде AB, равен половине дуги ACBD, то есть ∠ACB = 1/2 * 360° = 180°.
- Следовательно, ∠APB = 1/2 * ∠ACB = 1/2 * 180° = 90°.
Таким образом, мы доказали теорему о том, что вписанный угол ∠APB равен половине дуги ACBD. Эта теорема имеет важное значение в геометрии и широко применяется при решении различных задач.
Примеры вписанных углов
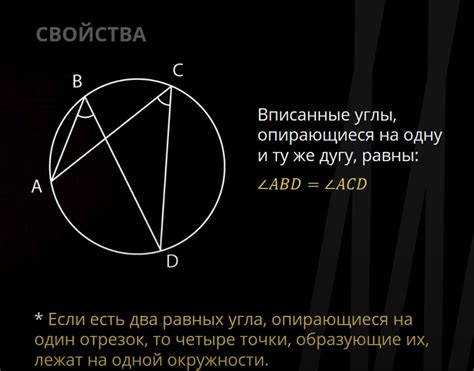
Рассмотрим несколько примеров вписанных углов:
Пример 1:
Пусть имеется окружность с центром O и радиусом r. Пусть AB и BC две хорды этой окружности, пересекающиеся в точке B. Тогда угол BAC, заключенный между хордами, называется вписанным углом.
Пример 2:
Пусть имеется окружность с центром O и радиусом r. Пусть CD - диаметр этой окружности, а AB - любая хорда, пересекающаяся с диаметром в точке E. Тогда угол ACE, заключенный между хордой и диаметром, также является вписанным углом.
Пример 3:
Пусть имеется окружность с центром O и радиусом r. Пусть AB - диаметр этой окружности, а CD - хорда, перпендикулярная диаметру AB и пересекающая его в точке E. Тогда угол CED, заключенный между диаметром и хордой, также является вписанным углом.
Обратите внимание, что каждый из этих вписанных углов равен половине меры дуги, соответствующей данному углу.
Зависимость величины вписанного угла от длины дуги
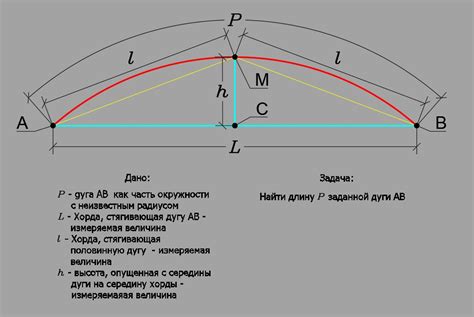
Один из основных принципов геометрии найти связь между длиной дуги и величиной вписанного угла на окружности. Это принцип очень полезен и находит применение в различных областях науки и техники.
Согласно теореме о вписанном угле, вписанный угол на окружности равен половине дуги, ограниченной этим углом и проведенной между точками, где эта дуга пересекает окружность. Другими словами, если у нас есть окружность с центром в точке O и радиусом r, и мы знаем длину дуги AB на этой окружности, мы можем найти величину вписанного угла AOB с помощью следующей формулы:
| Величина вписанного угла (в градусах) | Длина дуги (в радианах) |
|---|---|
$$\theta = \frac{180}{\pi} \cdot \frac{AB}{r}$$ | $$AB = \theta \cdot \frac{r}{180} \cdot \pi$$ |
Таким образом, зная длину дуги на окружности, мы можем легко вычислить величину вписанного угла. Эта формула особенно полезна при работе с окружностями и дугами в геометрии.
Построение вписанных углов на плоскости
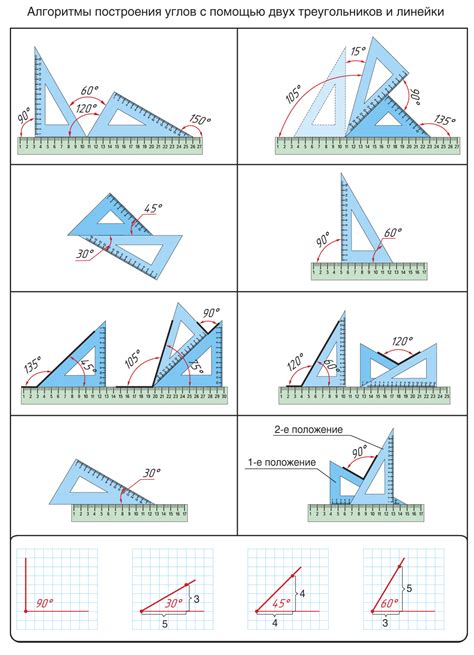
Для построения вписанного угла необходимо знать две точки на окружности, через которые будут проходить его стороны. Для этого можно использовать карандаш и циркуль. Провести окружность с центром в точке O и проходящую через точки A и B. Затем, с помощью циркуля, провести отрезки OA и OB. Их точки пересечения будут вершиной вписанного угла.
Вписанный угол имеет свойства, позволяющие найти его величину или угловую меру. Для этого можно использовать формулу:
- Вычислить длину дуги между точками A и B на окружности.
- Разделить длину дуги пополам.
- Полученное значение будет равно величине вписанного угла.
Таким образом, вписанный угол может быть построен и измерен с помощью окружности и рассчитан по формуле, основываясь на длине дуги. Это важное свойство углов на плоскости и находит применение в геометрии, астрономии и других науках.
Взаимосвязь вписанного угла и центрального угла
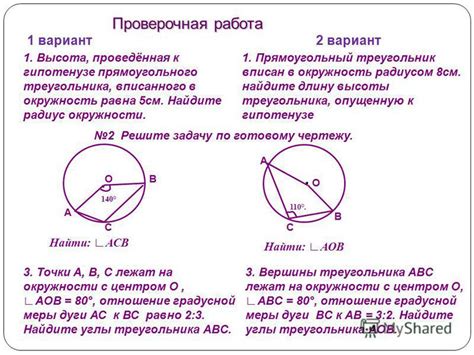
В математике вписанный угол и центральный угол имеют тесную взаимосвязь и связаны с дугами на окружности.
Вписанный угол определяется между двумя хордами, протянутыми на окружности. Этот угол равен половине меры дуги, заключенной между этими хордами.
Центральный угол определяется двумя лучами, выходящими из центра окружности и заключающими некоторую дугу. Мера центрального угла равна мере соответствующей вписанного угла, определенного той же дугой.
Таким образом, если у нас есть окружность с вписанным углом, то мера этого угла будет равна половине меры соответствующего центрального угла, а также равна половине меры дуги, заключенной между хордами, которые определяют вписанный угол.
Эта взаимосвязь между вписанным углом, центральным углом и дугой на окружности является очень важным свойством и находит применение в различных областях геометрии, физики и инженерии. Весьма полезно знать и использовать это свойство, чтобы решать задачи и находить решения в различных областях знаний.
Вписанные углы в геометрических формулах
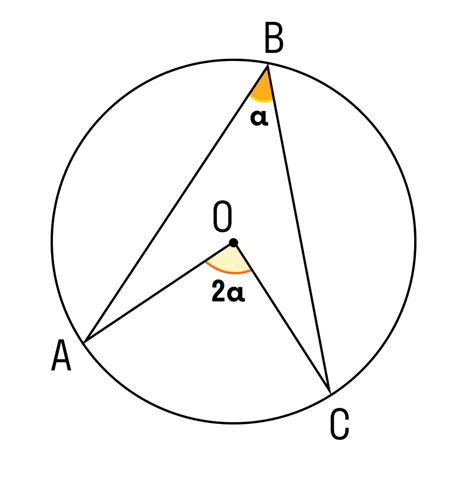
В геометрии широко используются понятия о вписанных углах. Вписанный угол определяется дугой, которую он охватывает на окружности. Важно знать, что вписанный угол равен половине дуги, которую он охватывает.
Если имеется окружность с центром в точке O и радиусом r, а две точки A и B находятся на этой окружности, то угол между хордой AB и касательной, проведенной из точки A или B, будет вписанным углом.
Существует простая формула для вычисления вписанного угла. Пусть α - угол в градусах, а L - длина дуги, которую охватывает данный угол на окружности. Тогда величина вписанного угла вычисляется по формуле:
| Формула для вписанного угла: |
|---|
| α = L/2r |
Зная радиус окружности и длину дуги, можно легко вычислить величину вписанного угла. Данная формула находит практическое применение при решении различных задач геометрии, связанных с окружностями.
Таким образом, вписанные углы являются важными элементами в геометрических формулах и имеют прямую связь с дугами, которые они охватывают. Понимание этого свойства углов позволяет более эффективно решать задачи и упрощает работу с геометрическими фигурами.
Практическое применение вписанных углов

Понимание свойств и характеристик вписанных углов имеет практическое применение в различных областях, включая геометрию, физику, инженерию и дизайн. В следующей таблице представлены некоторые примеры практического использования вписанных углов:
| Область применения | Пример |
|---|---|
| Геометрия | Вычисление радиуса окружности по известной длине дуги, а также в проблемах связанных с измерением и построением окружностей. |
| Физика | Расчет углов отражения и преломления света при прохождении через линзы и призмы. |
| Инженерия | Использование вписанных углов в проектировании механизмов и систем для определения движений и углов поворота. |
| Дизайн | Применение вписанных углов в графическом дизайне для создания более эстетически приятных и симметричных композиций и логотипов. |
Изучение и использование свойств вписанных углов не только помогает в понимании основ геометрии, но и является важным инструментом в различных практических задачах и приложениях.



