Математика, как наука, предлагает нам множество интересных и сложных вопросов, которые требуют глубокого понимания. Одним из таких вопросов является вопрос о сумме рациональных чисел - является ли она рациональным числом? Рациональные числа, как мы знаем, представляются в виде дробей, где числитель и знаменатель - целые числа, а знаменатель не равен нулю.
Итак, допустим, у нас есть два рациональных числа, представленные дробями: а = p/q и b = r/s, где p, q, r и s - целые числа, а s и q не равны нулю. Теперь посмотрим на их сумму: a + b = p/q + r/s.
Чтобы доказать, что сумма рациональных чисел является рациональным числом, мы должны показать, что сумма a + b также может быть представлена в виде дроби, у которой числитель и знаменатель являются целыми числами. Что ж, применим простое математическое преобразование к сумме: a + b = (p * s + q * r)/(q * s).
Следовательно, мы видим, что сумма a + b может быть представлена в виде дроби с числителем p * s + q * r и знаменателем q * s, которые являются целыми числами. Таким образом, сумма рациональных чисел также является рациональным числом!
Сумма рациональных чисел и их тип

Для начала рассмотрим пример: 1/2 + 1/3. Чтобы сложить эти две дроби, необходимо привести их к общему знаменателю. Общим знаменателем в данном случае является 6. После приведения к общему знаменателю получаем 3/6 + 2/6, что равно 5/6.
Из этого примера становится ясно, что сумма двух рациональных чисел также является рациональным числом. Это связано с тем, что в числителе и знаменателе суммы будет целое число, что и определяет рациональное число.
Обобщая этот результат, можно сказать, что сумма любого конечного количества рациональных чисел также будет рациональным числом. Это связано с особенностями дробной формы представления рациональных чисел.
Определение рациональных чисел
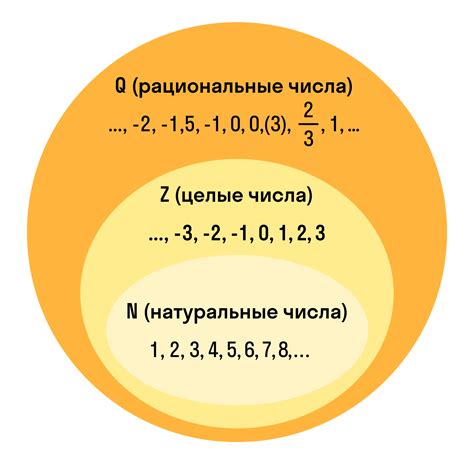
Формально, рациональные числа могут быть записаны в виде a/b, где a – числитель, b – знаменатель, и оба a и b являются целыми числами.
Например, числа -1, 0, 1, 2/3, -9/4 являются рациональными числами, так как они могут быть представлены в виде дробей.
Множество всех рациональных чисел обычно обозначается символом Q. Рациональные числа имеют ряд свойств, таких как коммутативность и ассоциативность операции сложения, умножение, деления и других.
| Символ | Описание |
|---|---|
| Q | Множество всех рациональных чисел |
| Z | Множество всех целых чисел |
| N | Множество всех натуральных чисел |
Из определения рациональных чисел следует, что сумма двух рациональных чисел также является рациональным числом. Если a/b и c/d – рациональные числа, то их сумма может быть записана как (ad + bc)/(bd), где ad + bc и bd являются целыми числами.
Сложение рациональных чисел

Рациональные числа - это числа, которые можно представить в виде дроби, где числитель и знаменатель являются целыми числами.
При сложении рациональных чисел сначала нужно привести их к общему знаменателю. Для этого находим наименьшее общее кратное знаменателей и приводим числа к этому знаменателю.
После приведения к общему знаменателю складываем числители и получаем новый числитель. Знаменатель остается неизменным.
Итак, сложение рациональных чисел происходит следующим образом: если у нас есть два рациональных числа с числителями a и b и одинаковыми знаменателями c, то их сумма равна дроби с числителем a + b и знаменателем c.
Таким образом, результат сложения двух рациональных чисел также является рациональным числом.
Доказательство рациональности суммы

Теперь посмотрим на сумму этих двух чисел: a + b = p/q + r/s = (ps + qr)/(qs).
Заметим, что числитель и знаменатель в полученной дроби также являются целыми числами, поскольку произведения целых чисел и суммы целых чисел сами являются целыми числами.
Таким образом, мы видим, что сумма двух рациональных чисел представляет собой дробь, в которой числитель и знаменатель являются целыми числами. То есть, сумма рациональных чисел также является рациональным числом.
Это доказывает, что при сложении двух рациональных чисел результат всегда будет рациональным числом.
Примеры рациональных чисел и их сумм

| Число 1 | Число 2 | Сумма чисел |
|---|---|---|
| 1/2 | 3/4 | 5/4 |
| 7/8 | 1/4 | 9/8 |
| 2/5 | 3/5 | 1 |
Рационализация суммы двух и более чисел

Для доказательства этого факта предположим, что у нас есть два рациональных числа $r_1$ и $r_2$. Мы можем их представить в виде дробей $\frac{a}{b}$ и $\frac{c}{d}$ соответственно, где $a$, $b$, $c$ и $d$ являются целыми числами.
Тогда мы можем записать сумму этих чисел как:
$$r_1 + r_2 = \frac{a}{b} + \frac{c}{d}$$
Чтобы сложить эти две дроби, мы должны привести их к общему знаменателю. Если мы умножим первую дробь на $\frac{d}{d}$ и вторую дробь на $\frac{b}{b}$, то получим:
$$r_1 + r_2 = \frac{a \cdot d}{b \cdot d} + \frac{c \cdot b}{d \cdot b}$$
Сокращая знаменатель каждой дроби до $bd$, мы получим:
$$r_1 + r_2 = \frac{a \cdot d + c \cdot b}{b \cdot d}$$
Таким образом, мы видим, что сумма двух рациональных чисел также будет представлять собой дробное число с целыми числами в числителе и знаменателе, что является определением рационального числа.
Также стоит отметить, что этот результат верен не только для суммы двух рациональных чисел, но и для суммы любого конечного числа рациональных чисел. Следовательно, сумма двух и более рациональных чисел всегда будет рациональным числом.



