В математике последовательность представляет собой упорядоченный набор чисел, исходя из определенных правил. Одним из основных свойств последовательности является ее сходимость, которая имеет важное значение при решении различных математических задач.
Сходимость последовательности означает, что ее элементы стремятся к определенному пределу по мере приближения к бесконечности. Другими словами, все члены последовательности становятся все ближе и ближе к некоторому числу, называемому пределом последовательности. Сходимость позволяет нам анализировать и предсказывать поведение последовательности в бесконечности.
Ограниченность последовательности – это еще одно важное свойство, которое гарантирует, что все элементы последовательности находятся в некотором ограниченном диапазоне значений. Это означает, что существует верхняя и нижняя границы, между которыми находятся все члены последовательности. Ограниченность позволяет нам определить, какие значения может принимать последовательность и как она будет вести себя в бесконечности.
Таким образом, сходимость и ограниченность являются ключевыми свойствами последовательности, которые позволяют нам анализировать и предсказывать ее поведение. Знание этих свойств позволяет решать различные задачи в математике и приложениях, а также строить более сложные теории и модели.
Почему математическая последовательность сходится?

Математическая последовательность сходится, когда значения её членов приближаются к некоторому пределу при увеличении номеров членов последовательности. То есть, существует число, которому бесконечно много членов последовательности становятся сколь угодно близкими.
Одна из основных причин сходимости последовательности – ограниченность. Если все члены последовательности ограничены сверху и снизу, то эта последовательность является ограниченной. Ограниченные последовательности могут иметь предел, к которому они сходятся.
Также, последовательности сходятся при условии монотонности. Если последовательность возрастающая и ограничена сверху, или убывающая и ограничена снизу, то она имеет предел и сходится.
Сходимость последовательности может быть доказана через определение предела и использование соответствующих математических методов, таких как оценка снизу и сверху, теорема о двух милиционерах или теорема Коши.
Изучение сходимости последовательностей является важной областью математического анализа и находит применение в различных областях современной науки, включая физику, экономику и информатику.
Определение и свойства сходящейся последовательности

Формально, последовательность чисел {an} сходится к числу L, если для любого положительного числа ε существует номер N, начиная с которого все элементы последовательности, начиная с номера N, лежат в пределах от L - ε до L + ε.
Сходимость последовательности обладает несколькими свойствами:
| Свойство | Описание |
| Ограниченность | Сходящаяся последовательность является ограниченной, то есть существует такое число M, что все элементы последовательности лежат в пределах от -M до M. |
| Единственность предела | Если последовательность сходится, то ее предел единственный, то есть для любых двух предполагаемых пределов L и L' L ≠ L'. |
| Арифметические операции | Последовательности, сходящиеся к числам L и L', сходятся к одинаковому пределу при выполнении арифметических операций над ними. |
| Монотонность | Монотонная ограниченная последовательность является сходящейся. |
Сходимость последовательности является важным понятием в математике и используется в доказательствах и решении различных задач. Понимание определения и свойств сходящихся последовательностей позволяет более глубоко изучать и применять математические концепции.
Ограниченность последовательности и ее связь с сходимостью

Последовательность чисел сходится, если ее элементы стремятся к определенному пределу. Если последовательность ограничена, это означает, что все ее элементы находятся в определенном диапазоне значений.
Ограниченность последовательности является необходимым условием для ее сходимости. Если последовательность не является ограниченной, то она не может сходиться к какому-либо пределу.
Ограниченность последовательности может быть определена с помощью двух критериев: верхней и нижней границы.
- Верхняя граница - это такое число, которое больше или равно всем элементам последовательности. Если последовательность имеет верхнюю границу, она называется ограниченной сверху.
- Нижняя граница - это такое число, которое меньше или равно всем элементам последовательности. Если последовательность имеет нижнюю границу, она называется ограниченной снизу.
Если последовательность имеет одновременно верхнюю и нижнюю границу, она будет ограниченной. В этом случае, она будет иметь определенный интервал значений, в пределах которого находятся все ее элементы.
Если последовательность не является ограниченной, это означает, что ее элементы могут стремиться к бесконечности или расходиться. В таком случае, она не будет сходиться к какому-либо пределу.
Таким образом, ограниченность последовательности является важным критерием для ее сходимости. Ограниченная последовательность может иметь предел, к которому ее элементы стремятся, в то время как неограниченная последовательность не будет сходиться к какому-либо пределу.
Различные виды сходимости последовательностей

1. Сходимость к конечному пределу: Последовательность сходится к конечному пределу, если все её элементы стремятся к определенному числу. В таком случае говорят, что последовательность ограничена.
2. Бесконечная сходимость: Если последовательность не имеет конечного предела, но её элементы стремятся к бесконечности, то говорят о бесконечной сходимости. Например, последовательность {n} = 1, 2, 3, ... имеет бесконечный предел.
3. Сходимость к плюс или минус бесконечности: Если последовательность имеет предел плюс или минус бесконечность, то говорят о сходимости к плюс или минус бесконечности соответственно.
4. Частичная сходимость: Если у последовательности есть подпоследовательность, сходящаяся к конечному или бесконечному пределу, но сама последовательность не сходится, то говорят о частичной сходимости.
5. Поточечная сходимость: Для последовательности функций поточечная сходимость означает, что значения функций в точках последовательности сходятся к значениям предельной функции. Например, если последовательность функций f_n(x) сходится к функции f(x), то при каждом фиксированном x последовательность значений f_n(x) сходится к значению f(x).
Указанные выше виды сходимости последовательностей являются лишь некоторыми примерами, и существует и другие виды сходимости, такие как равномерная сходимость и сходимость по мере.
Односторонняя и двусторонняя ограниченность последовательности

Существуют два типа ограниченности последовательности: односторонняя и двусторонняя. Односторонняя ограниченность означает, что элементы последовательности находятся либо строго выше некоторого значения, либо строго ниже него. Например, последовательность {1, 2, 3, 4, ...} является односторонне ограниченной, так как все ее элементы больше или равны 1.
Двусторонняя ограниченность предполагает, что элементы последовательности находятся как выше, так и ниже некоторых границ. Например, последовательность {-2, -1, 0, 1, 2, ...} является двухсторонне ограниченной, так как все ее элементы находятся в пределах от -2 до 2.
Ограниченность последовательности является важным свойством при доказательстве ее сходимости. Если последовательность ограничена, то можно утверждать, что она сходится к некоторому пределу. В противном случае, если последовательность не ограничена, она считается расходящейся и не имеет предела.
Односторонняя и двусторонняя ограниченность последовательности позволяют устанавливать верхние и нижние границы ее элементов и определять, сходится ли последовательность и к какому значению. Эти понятия являются фундаментальными при изучении математического анализа и анализа сходимости последовательностей.
Критерий Коши для сходимости последовательности

Формально, последовательность {an} сходится к пределу A, если для любого положительного числа ε найдется такое натуральное число N, что для любых натуральных чисел n, m больших N, выполнено неравенство |an - am| < ε.
Таким образом, идея Критерия Коши заключается в том, что элементы последовательности со временем становятся все ближе и ближе друг к другу, что говорит о ее сходимости.
| Пример | Объяснение |
|---|---|
| Последовательность {1/n} | Для любого ε > 0 можно найти такой номер N (например, N = 1/ε), начиная с которого все элементы последовательности отличаются от предыдущих элементов на величину меньшую, чем ε. |
| Последовательность {(-1)^n} | Для любого ε > 0 можно найти такой номер N (например, N = 2), начиная с которого все элементы последовательности отличаются от предыдущих элементов на величину меньшую, чем ε. |
Таким образом, Критерий Коши является важным инструментом для доказательства сходимости последовательностей. Он позволяет установить, что последовательность не только сходится, но и имеет конечный предел, что является важным свойством в анализе и математической физике.
Закон больших чисел и сходимость последовательности

Сходимость последовательности - это свойство, которое означает, что значения этой последовательности сходятся к определенному числу. Если последовательность является ограниченной, то она также сходится. Ограниченность последовательности означает, что существуют числа, между которыми находятся все элементы последовательности.
В контексте закона больших чисел, для того чтобы последовательность сходилась, она должна быть ограничена. Если последовательность не ограничена, то величина выборок может изменяться в широких пределах и справедливость закона больших чисел не будет выполняться.
Таким образом, для того чтобы быть уверенными в сходимости последовательности, нужно убедиться в ее ограниченности. Это позволит применять закон больших чисел для более точных вычислений и прогнозов на основе выборочных данных.
Влияние начального члена на сходимость последовательности

Начальный член последовательности играет важную роль в ее сходимости. Он определяет, какие значения будут близкими к последующим членам и как быстро последовательность сойдется к своему пределу.
Если начальный член достаточно близок к пределу последовательности, то она сойдется быстро. Это можно объяснить тем, что более близкие значения напрямую влияют на выбор следующих членов. В этом случае разница между значениями последовательности будет уменьшаться с каждым шагом, и она быстро приблизится к пределу.
Если же начальный член находится далеко от предела последовательности, то она может сходиться медленно или даже расходиться. Это связано с тем, что большие различия между значениями последовательности могут замедлить сходимость и привести к ее разбеганию.
Важно иметь в виду, что начальный член не всегда определяет сходимость последовательности. Иногда последовательность может сходиться даже при больших начальных значениях, если разность между членами последовательности уменьшается достаточно быстро. Однако выбор близкого начального члена может значительно ускорить процесс сходимости.
Таким образом, выбор начального члена является важным шагом при анализе сходимости последовательности. Чтобы ускорить процесс сходимости, рекомендуется выбирать начальный член, близкий к пределу последовательности.
Функция, ограниченная на последовательности
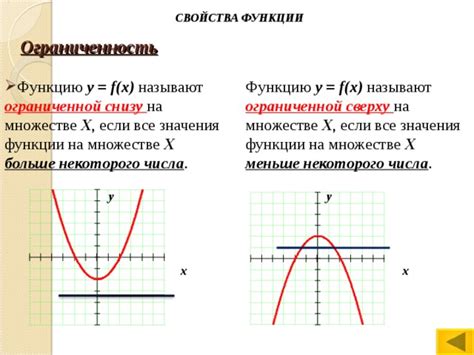
Когда говорят о последовательности, которая сходится и ограничена, часто возникает вопрос, как это связано с функцией, которая определена на этой последовательности.
Функция, ограниченная на последовательности, имеет конечную верхнюю и нижнюю границы. Это означает, что значения функции, определенной на всех элементах последовательности, не превышают некоторой конечной величины.
Когда последовательность является ограниченной, функция, определенная на этой последовательности, также будет ограниченной. Это означает, что значения функции будут ограничены как сверху, так и снизу. Например, если последовательность ограничена сверху числом M и снизу числом m, то функция будет ограничена сверху числом M и снизу числом m.
Сходимость последовательности в пространстве функций

При изучении сходимости последовательностей мы обычно рассматриваем числовые последовательности, но также возможна сходимость в пространстве функций. Например, мы можем рассматривать последовательности функций, которые сходятся к определенной функции в некоторой области определения.
Для определения сходимости последовательности функций в пространстве функций, мы можем использовать те же критерии, что и для числовых последовательностей. Например, последовательность функций сходится равномерно, если разность между каждой функцией и предельной функцией становится сколь угодно малой при достаточно больших значениях независимой переменной.
Ограниченность последовательности функций в пространстве функций имеет особое значение, поскольку это показывает, что все функции в последовательности ограничены сверху и снизу на некоторой области определения. Из ограниченности последовательности функций следует, что она содержит отдельные функции, которые также ограничены.
Сходимость и ограниченность последовательности функций в пространстве функций могут быть доказаны с использованием различных методов, таких как применение критерия Коши или сходимости почленного ряда. Кроме того, сходимость последовательности функций может быть связана с ее равномерной непрерывностью и другими свойствами функций.
Изучение сходимости последовательности функций в пространстве функций является важным аспектом математического анализа и имеет широкий спектр применений в различных областях, таких как теория вероятностей, дифференциальные уравнения и физика.



