Математика, безусловно, является одной из фундаментальных наук, на которой базируются многие другие научные и технические дисциплины. Она предоставляет нам мощный инструментарий для решения разнообразных задач и позволяет нам познавать законы и структуру окружающего мира. В числе многих других операций, которые математика предоставляет нам, важной является вычисление корней. Но, откуда взялась частая поговорка "нет нуля под корнем"?
Для начала, давайте вспомним определение корня. Корень из числа a это такое число x, которое возведенное в степень n дает a. В математической записи это можно представить как x^n = a. Но что произойдет, если мы попробуем вычислить корень из отрицательного числа?
Мы сталкиваемся с одним из основных ограничений математики - отрицательное число, взятое в нечетную степень, всегда будет отрицательным. И такое число не может быть результатом извлечения корня, так как корни - это числа, которые возводятся в четную степень. Именно поэтому мы говорим, что "нет нуля под корнем".
Особенности математических операций
Одна из таких особенностей – отсутствие нуля под корнем. Корень из отрицательного числа не определен в области действительных чисел. Например, корень из -9 не имеет решения в множестве действительных чисел. Это связано с фундаментальной характеристикой действительных чисел – положительностью квадрата числа.
Другой особенностью является деление на ноль. Деление на ноль также не определено в области действительных чисел. Это связано с тем, что нельзя разделить число на ноль без введения понятия бесконечности. В математике есть понятие бесконечности, но оно не является числом и не может быть результатом вычислений при обычных операциях.
Еще одной особенностью является деление нуля на ноль. Решение такого выражения не определено и считается неопределенным значением. Когда мы делим ноль на ноль, мы можем получить любое число или даже неопределенное значение, в зависимости от контекста задачи.
Это лишь некоторые из множества особенностей, которые существуют в математических операциях. Знание этих особенностей поможет нам избежать ошибок и правильно проводить вычисления.
| Операция | Определение |
|---|---|
| Сложение | Действие, при котором два числа объединяются в одно число |
| Вычитание | Действие, при котором из одного числа вычитается другое число |
| Умножение | Действие, при котором одно число увеличивается в несколько раз |
| Деление | Действие, при котором одно число делится на другое число |
Корень из нуля

Математика дает нам множество инструментов для работы с числами, однако есть некоторые особенности, которые необходимо учитывать. Одна из таких особенностей связана с корнем из нуля. В отличие от других чисел, корень из нуля не определен.
При вычислении корня из числа мы ищем такое число, возведенное в данную степень, чтобы получить исходное число. Но, если мы возведем ноль в любую положительную степень, результатом будет всегда ноль. Ноль не имеет других положительных степеней, кроме нулевой степени, и поэтому корней у нуля нет.
Эту особенность можно объяснить чисто логически. Ноль не содержит информации о каком-либо количестве или мере, он представляет отсутствие числа. Поэтому, попытка извлечения корня из нуля не имеет смысла.
Если вам понадобится вычислить корень квадратный из числа, убедитесь, что это число положительное. В противном случае, результатом будет неопределенное значение.
Мнимые числа
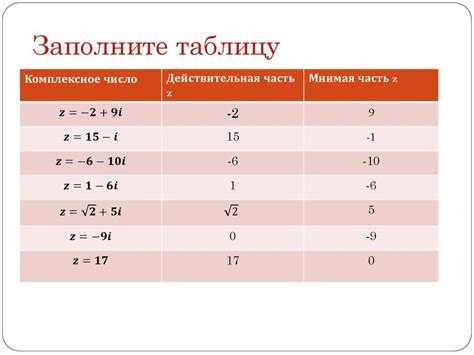
Мнимые числа широко используются в математике и естественных науках, особенно в тех случаях, когда решение уравнений, содержащих квадратные корни, имеет мнимую составляющую. Мнимые числа позволяют работать с такими уравнениями и выполнять различные операции, которые иначе были бы невозможны или не имели никакого смысла.
Мнимые числа представляются в виде суммы действительной и мнимой частей: a + bi, где a и b – действительные числа, а i – мнимая единица. Например, комплексное число 3 + 4i имеет действительную часть 3 и мнимую часть 4i.
Основные операции с мнимыми числами включают сложение, вычитание, перемножение и деление. Например, сумма двух комплексных чисел вычисляется путем сложения их действительных и мнимых частей по отдельности.
| Операция | Формула |
|---|---|
| Сложение | (a + bi) + (c + di) = (a + c) + (b + d)i |
| Вычитание | (a + bi) - (c + di) = (a - c) + (b - d)i |
| Умножение | (a + bi)(c + di) = (ac - bd) + (ad + bc)i |
| Деление | (a + bi) / (c + di) = [(ac + bd) / (c^2 + d^2)] + [(bc - ad) / (c^2 + d^2)]i |
Мнимые числа не имеют порядка и не могут быть отсортированы по возрастанию или убыванию. Однако, они могут быть представлены на комплексной плоскости, где действительная часть отмечается по оси абсцисс, а мнимая часть – по оси ординат.
В заключении, мнимые числа играют важную роль в математике и науке, расширяя область применимости и возможностей чисел и операций. Они позволяют работать с уравнениями и моделями, которые ранее были недоступны или сложны для решения.
Деление на ноль

Деление на ноль нарушает основные правила арифметики и приводит к противоречиям. Рассмотрим пример: если мы разделим число на ноль и получим конечное число, то перемножив его на ноль мы получим исходное число, что является противоречием с определением деления.
Также деление на ноль является неопределенной операцией. Из-за этого любое математическое выражение с делением на ноль, включая корень из нуля, не имеет смысла.
Важно отметить, что в программировании деление на ноль также ведет к ошибке. В языках программирования, таких как Java или Python, при попытке выполнить деление на ноль возникает исключение или ошибка деления на ноль.
Возведение в нулевую степень

Нетрудно заметить, что для любого числа x следующие равенства справедливы:
| Степень | Результат |
|---|---|
| x0 | 1 |
| x1 | x |
| x2 | x * x |
| x3 | x * x * x |
| xn | x * x * ... * x (n раз) |
Правило возведения в нулевую степень просто продолжает эту последовательность. Если продолжить ее, то можно увидеть следующее:
| Степень | Результат |
|---|---|
| x0 | 1 |
| x1 | x |
| x2 | x * x |
| x3 | x * x * x |
| x4 | x * x * x * x |
| ... | ... |
| xn | x * x * ... * x (n раз) |
| x0 | 1 |
Таким образом, в математике определено, что любое число, возведенное в степень 0, равно 1. Это правило можно использовать в формулах, уравнениях, а также в более сложных математических операциях.
Арифметические операции

К основным арифметическим операциям относятся:
- Сложение – операция, которая позволяет складывать два или более числа. Результатом сложения двух чисел является их сумма.
- Вычитание – операция, которая позволяет вычитать одно число из другого. Результат разности двух чисел называется разностью.
- Умножение – операция, которая позволяет умножать два или более числа. Результат умножения двух чисел называется произведением.
- Деление – операция, которая позволяет делить одно число на другое. Результат деления двух чисел называется частным. Обратной операцией к делению является умножение.
Кроме основных арифметических операций существуют и дополнительные операции, такие как возведение в степень, извлечение корня и т. д.
При выполнении арифметических операций необходимо учитывать правила приоритета операций, так как порядок выполнения операций может влиять на результат.
Операции сложения и умножения являются коммутативными, то есть порядок операндов не важен. Например, 2 + 3 = 3 + 2 и 2 * 3 = 3 * 2.
Деление и вычитание не являются коммутативными операциями. Например, 2 - 3 ≠ 3 - 2 и 2 ÷ 3 ≠ 3 ÷ 2.
Помимо арифметических операций с числами, существуют и операции со специальными значениями, такими как бесконечность (∞) и неопределенность (например, деление на ноль).
Важно помнить, что при делении на ноль результатом является неопределенность, поэтому нет возможности извлечь корень из нуля.
Таким образом, отсутствие нуля под корнем обусловлено особенностями математических операций и правилами их выполнения.
Сложение и вычитание дробей

При сложении и вычитании дробей необходимо привести их к общему знаменателю. Это делается путем нахождения наименьшего общего кратного (НОК) знаменателей. Затем числители дробей складываются или вычитаются в зависимости от выбранной операции.
Пример:
Допустим, у нас есть две дроби: 1/3 и 1/4. Найдем их общий знаменатель:
Знаменатель первой дроби - 3, знаменатель второй дроби - 4. НОК(3, 4) = 12.
Получаем две дроби с общим знаменателем: 4/12 и 3/12. Далее, складываем их числители:
4/12 + 3/12 = 7/12.
Таким образом, сумма двух дробей 1/3 и 1/4 равна 7/12.
Вычитание дробей выполняется аналогично. Если нужно вычесть дробь из другой дроби, необходимо привести их к общему знаменателю и вычесть числители.
Например:
Допустим, у нас есть две дроби: 1/2 и 1/5. Найдем их общий знаменатель:
Знаменатель первой дроби - 2, знаменатель второй дроби - 5. НОК(2, 5) = 10.
Получаем две дроби с общим знаменателем: 5/10 и 2/10. Далее, вычитаем числители:
5/10 - 2/10 = 3/10.
Таким образом, разность двух дробей 1/2 и 1/5 равна 3/10.
Умножение и деление дробей
Умножение дробей происходит путем умножения числителей и знаменателей отдельно. Например, для умножения дробей 1/2 и 3/4 нужно умножить числитель 1 на числитель 3 и знаменатель 2 на знаменатель 4. Получится дробь 3/8.
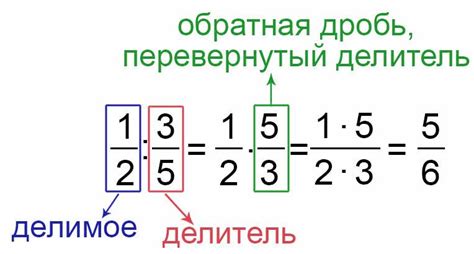
Деление дробей происходит путем умножения первой дроби на обратную второй дробь. Обратная дробь получается путем переворачивания числителя и знаменателя. Например, для деления дробей 2/3 на 4/5 нужно умножить 2/3 на обратную дробь 5/4. После умножения получится дробь 10/12, которую можно еще упростить до 5/6.
Важно помнить, что деление на ноль запрещено в математике, поэтому нельзя делить на ноль ни числитель, ни знаменатель дроби. Если в дроби имеется ноль в числителе или знаменателе, дробь становится неопределенной.
Функция модуля
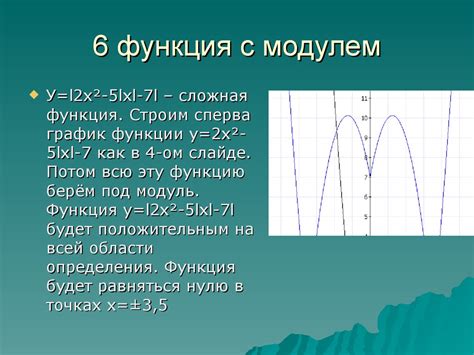
Функция модуля имеет следующее свойство: |x| = x, если x ≥ 0, и |x| = -x, если x
Функция модуля широко используется в различных областях математики, физики, программирования и других наук. Например, она может использоваться для нахождения расстояния между двумя точками на числовой оси или для определения модуля числа в программе.
Применение функции модуля также связано с определенными особенностями. Например, в уравнениях или неравенствах, содержащих функцию модуля, могут возникать различные случаи решений в зависимости от знака исходного числа. Кроме того, функция модуля может быть использована для определения экстремумов функций и нахождения производной по определенным правилам.
Математические операции в программировании

В программировании, как и в математике, существуют различные операции для работы с числами. Основные математические операции, которые можно использовать в программировании, включают сложение, вычитание, умножение и деление.
Сложение - это операция, которая позволяет суммировать два числа. Например, если у нас есть числа 5 и 3, то результатом сложения будет число 8.
Вычитание - это операция, которая позволяет вычесть одно число из другого. Например, если у нас есть число 10 и мы вычитаем из него число 5, то результатом будет число 5.
Умножение - это операция, которая позволяет умножить одно число на другое. Например, если у нас есть числа 4 и 2, то результатом умножения будет число 8.
Деление - это операция, которая позволяет разделить одно число на другое. Например, если у нас есть число 10 и мы разделим его на число 2, то результатом будет число 5.
В программировании также существуют другие математические операции, такие как возведение в степень, нахождение остатка от деления и другие. Однако основные операции сложения, вычитания, умножения и деления являются основой для выполнения более сложных математических операций.
При выполнении математических операций в программировании очень важно учитывать правила математики и порядок выполнения операций. Например, при использовании операций сложения и вычитания, сначала выполняются операции в скобках, затем умножение и деление, и только потом сложение и вычитание. Это позволяет получать правильные результаты и избегать ошибок.



