Параллелограмм – это геометрическая фигура, которая обладает множеством интересных свойств. Одно из самых удивительных по своей простоте и важности является тот факт, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Это правило, которое можно математически доказать и легко проверить на практике.
Чтобы понять, почему так происходит, давайте представим себе параллелограмм с произвольными сторонами и диагоналями. Возьмем его левый верхний угол и проведем из него две диагонали – одну вправо и вниз, а вторую влево и вниз. Обозначим длину верхней стороны параллелограмма как a, а боковой стороны – b.
Теперь мы можем приступить к самому интересному моменту. Если мы посчитаем квадрат длины каждой стороны параллелограмма и сложим их, то получим следующее: a^2 + b^2 + a^2 + b^2 = 2a^2 + 2b^2. Аналогично, если мы посчитаем квадрат длины каждой диагонали параллелограмма и сложим их, то получим следующее: (a + b)^2 + (a - b)^2 = a^2 + 2ab + b^2 + a^2 - 2ab + b^2 = 2a^2 + 2b^2. Очевидно, что оба результата равны между собой.
Таким образом, мы доказали, что сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Это правило может быть использовано при решении разнообразных задач и определении свойств параллелограммов. Интересно отметить, что оно также применимо к другим многоугольникам, например, прямоугольникам и ромбам.
Сумма квадратов диагоналей параллелограмма
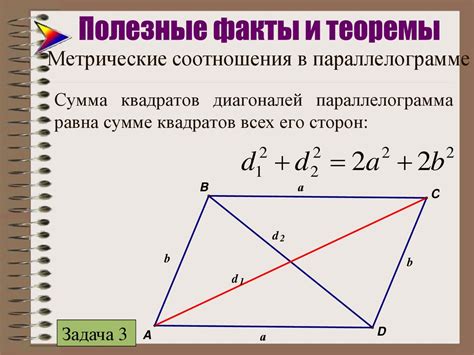
У параллелограмма есть две диагонали – прямые линии, соединяющие противоположные вершины. Одна диагональ делит параллелограмм на два треугольника, а вторая диагональ делит его на другие два треугольника.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон. Данное утверждение называется теоремой о сумме квадратов диагоналей параллелограмма.
Таким образом, если обозначить стороны параллелограмма как a и b, а диагонали как c и d, то утверждение можно записать как:
c^2 + d^2 = a^2 + b^2
Другими словами, сумма квадратов длин диагоналей равна сумме квадратов длин сторон параллелограмма.
Теорема о сумме квадратов диагоналей параллелограмма может использоваться для вычисления длины диагоналей по известным сторонам и наоборот.
Это утверждение имеет практическое применение в геометрии, физике, инженерии и других науках, где изучаются фигуры и их свойства.
Диагонали параллелограмма и их свойства

- Диагонали параллелограмма делятся пополам
- Диагонали параллелограмма пересекаются в точке, делящей их в отношении 1:1
- Сумма квадратов диагоналей равна сумме квадратов сторон
Каждая диагональ параллелограмма делит его на две равные части. Это означает, что отрезки, соединяющие середины противоположных сторон, равны по длине.
Точка пересечения диагоналей параллелограмма делит каждую из них в отношении 1:1. Это означает, что расстояние от середины одной диагонали до точки пересечения равно расстоянию от точки пересечения до середины другой диагонали.
Удивительное свойство диагоналей параллелограмма заключается в том, что сумма квадратов их длин равна сумме квадратов длин сторон параллелограмма. Это можно математически доказать и является основным свойством параллелограмма.
Эти свойства диагоналей параллелограмма позволяют использовать их в различных математических задачах и вычислениях.
Квадраты длин сторон параллелограмма
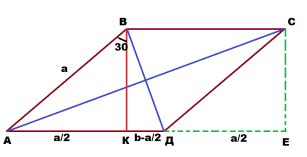
Пусть AB, BC, CD и DA - стороны параллелограмма. Обозначим их длины как a, b, c и d соответственно. Чтобы найти квадраты длин сторон, нам нужно возвести каждую длину в квадрат.
Квадрат длины стороны AB: a2
Квадрат длины стороны BC: b2
Квадрат длины стороны CD: c2
Квадрат длины стороны DA: d2
Сумму квадратов длин сторон параллелограмма можно выразить следующим образом:
a2 + b2 + c2 + d2
Так как противоположные стороны параллельны и равны по длине, диагонали параллелограмма также равны по длине. Пусть AC и BD - диагонали параллелограмма. Их длины обозначим как p и q соответственно.
По теореме Пифагора для треугольников ABC и CDA:
AC2 = AB2 + BC2 (1)
AC = √(a2 + b2) (2)
По теореме Пифагора для треугольников ABD и BCD:
BD2 = AB2 + BC2 (3)
BD = √(c2 + d2) (4)
Квадраты длин диагоналей можно выразить следующим образом:
Квадрат длины диагонали AC: p2 = a2 + b2
Квадрат длины диагонали BD: q2 = c2 + d2
Теперь мы можем сравнить сумму квадратов длин сторон (a2 + b2 + c2 + d2) с суммой квадратов длин диагоналей (p2 + q2). Мы видим, что они равны:
a2 + b2 + c2 + d2 = p2 + q2
Таким образом, мы доказали, что сумма квадратов длин сторон параллелограмма равна сумме квадратов длин его диагоналей.
Сумма квадратов длин диагоналей
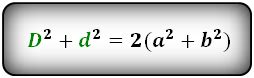
Для доказательства данного свойства можно воспользоваться теоремой Пифагора, которая устанавливает связь между длинами сторон и диагоналей прямоугольного треугольника.
Пусть AB и CD - стороны параллелограмма, а AC и BD - его диагонали. Согласно теореме Пифагора, сумма квадратов длин сторон параллелограмма AB и CD равна квадрату длины его диагоналей:
AB^2 + CD^2 = AC^2 + BD^2
Это свойство может быть использовано для нахождения длин диагоналей параллелограмма, если известны длины его сторон, или наоборот, для нахождения длин сторон, если известны длины диагоналей.
Кроме того, сумма квадратов длин диагоналей параллелограмма может быть использована для определения его свойств, таких как площадь, углы и высота.
Свойство суммы квадратов длин диагоналей параллелограмма является ключевым при изучении и применении данной фигуры в геометрии и математике в целом.
Доказательство равенства суммы квадратов

Для доказательства равенства суммы квадратов диагоналей параллелограмма и суммы квадратов его сторон, рассмотрим параллелограмм ABCD.
Пусть AB и CD - параллельные стороны параллелограмма, а AC и BD - диагонали.
Согласно теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
AC² = AB² + BC²
BD² = AB² + CD²
Поскольку AB = CD и BC = AD (по свойству параллелограмма), мы можем заменить соответствующие значения:
AC² = AD² + BC²
BD² = AD² + BC²
Просуммируем полученные уравнения:
AC² + BD² = AD² + BC² + AD² + BC²
Сократим одинаковые слагаемые:
AC² + BD² = 2(AD² + BC²)
Таким образом, мы доказали, что сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.
Примеры параллелограммов
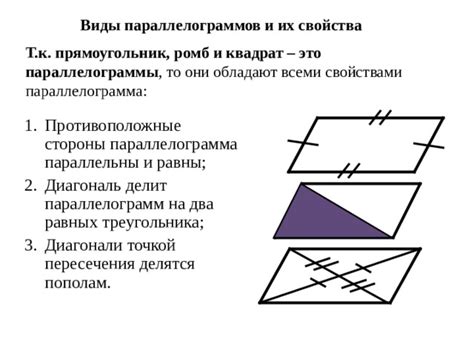
В геометрии существует множество примеров параллелограммов, которые иллюстрируют свойство равенства суммы квадратов диагоналей и суммы квадратов сторон.
| Тип параллелограмма | Сумма квадратов диагоналей | Сумма квадратов сторон |
|---|---|---|
| Прямоугольник | a^2 + b^2 | a^2 + b^2 |
| Ромб | 4d^2 | 4a^2 |
| Квадрат | 2a^2 | 4a^2 |
| Произвольный параллелограмм | 2(a^2 + b^2 + 2ab cos α) | 2(a^2 + b^2) |
Приведенные примеры подтверждают, что в любом параллелограмме сумма квадратов диагоналей равна сумме квадратов его сторон. Это свойство может быть использовано для доказательства различных геометрических утверждений о параллелограммах.
Почему сумма квадратов диагоналей равна сумме квадратов сторон
Для понимания, почему сумма квадратов диагоналей равна сумме квадратов сторон, рассмотрим параллелограмм ABCD:
Перед нами параллелограмм со сторонами AB, AD, BC и CD. Мы можем обозначить данные стороны как a, b, c и d соответственно.
Также у нас есть две диагонали: AC и BD. Давайте обозначим их как p и q.
Согласно теореме Пифагора, в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. В параллелограмме ABCD, диагонали - это гипотенузы прямоугольных треугольников, образованных сторонами и диагоналями.
Рассмотрим треугольник ACD. Его гипотенуза - диагональ AC, а катеты - стороны AD и CD. Согласно теореме Пифагора:
AC^2 = AD^2 + CD^2
Аналогично, для треугольника ABC справедлива следующая формула:
BC^2 = AB^2 + AC^2
Заметим, что можно выразить AC в первом уравнении, а затем подставить это выражение во второе уравнение:
BC^2 = AB^2 + (AD^2 + CD^2)
Мы можем переписать это уравнение, используя обозначенные стороны:
BC^2 = a^2 + (b^2 + c^2)
Аналогично, рассмотрим треугольник ABD с диагональю BD:
BD^2 = AB^2 + AD^2
Заметим, что AD^2 и AB^2 есть в обоих уравнениях. Можем выразить их, используя первое и второе уравнение:
AD^2 = AC^2 - CD^2
AB^2 = BC^2 - AC^2
Подставим эти выражения в уравнение для BD^2:
BD^2 = (BC^2 - AC^2) + (AC^2 - CD^2)
Заметим, что AC^2 и -AC^2 в этом уравнении взаимно уничтожаются:
BD^2 = BC^2 - CD^2
Используя обозначения сторон, перепишем это уравнение:
BD^2 = a^2 + c^2
Мы получили, что квадрат диагонали BD равен сумме квадратов сторон a и c.
Аналогично, вы можете провести серию аналогичных выкладок и получить, что квадрат диагонали AC также равен сумме квадратов сторон b и d:
AC^2 = b^2 + d^2
Таким образом, сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
AC^2 + BD^2 = a^2 + b^2 + c^2 + d^2
Иначе можно выразить:
AC^2 + BD^2 = AB^2 + BC^2 + CD^2 + AD^2
Это свойство не только помогает нам понять геометрию параллелограмма, но также находит применение в решении различных задач в математике и физике.
Применения данного свойства

Свойство о равенстве суммы квадратов диагоналей параллелограмма и суммы квадратов его сторон находит применение в различных областях геометрии и физики:
1. Геометрия. Данное свойство позволяет упростить вычисления и доказательства в задачах, связанных с параллелограммами. Например, при определении площади параллелограмма или при поиске сторон и углов фигуры по известным данным.
2. Физика. В физике параллелограммы могут использоваться для моделирования различных видов движения или сил. Например, в механике параллелограмм может служить для описания движения частицы в плоскости, а в электростатике - для представления диаграммы Кельвина.
3. Графика. Для создания и анимации различных геометрических фигур в компьютерной графике можно использовать параллелограммы и их свойства. Знание равенства суммы квадратов диагоналей и сторон может помочь в расчете координат и размеров фигур.
4. Строительство. В архитектуре и строительстве параллелограммы могут использоваться для создания нестандартных форм зданий и сооружений. Понимание свойств этих фигур помогает участникам проекта принимать правильные решения по расположению и пропорциям конструкций.
Все эти области деятельности находят применение в реальной жизни, поэтому понимание данного свойства параллелограммов является важным для получения универсальных навыков решения задач и работы с геометрическими объектами.




